S+20250812测试
A. 炫彩染色
只有两种情况,从0开始和从1开始,枚举秒了(
#include<bits/stdc++.h>
using namespace std;
#define intc const int
#define intl long long
#define Cios ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
int n;
string s;
signed main() {
Cios;
cin>>s;
n=s.length();
s=" "+s;
int now=1,ans1=0,ans2=0;
for (int i=1;i<=n;i++) {
if (s[i]-'0'!=now) ans1++;
now=!now;
}
now=0;
for (int i=1;i<=n;i++) {
if (s[i]-'0'!=now) ans2++;
now=!now;
}
cout<<min(ans1,ans2);
return 0;
}B. 寻找饼干
寻找四个角的饼干;如果吃的饼干不在角上最好,但是如果在,因为只可能少一个,所以肯定有一条对角线是完整的。可以发现,寻找到的两条对角线中,所标出的矩形更大的一定是正确的。如图:
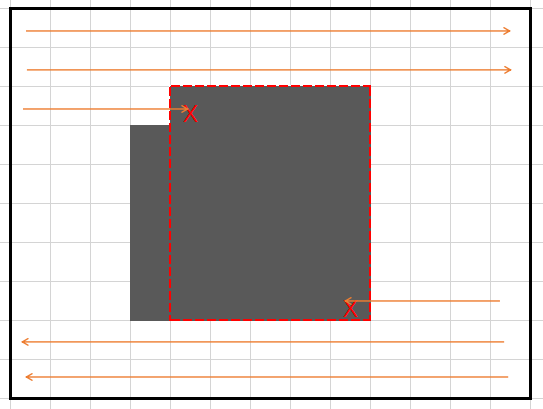
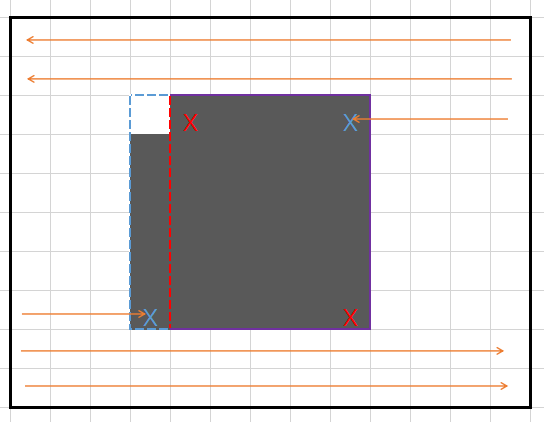
所以使用四种方法枚举,找出矩形,之后枚举矩形内部找少的那个点即可。
#include<bits/stdc++.h>
using namespace std;
#define intc const int
#define intl long long
#define Cios ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define out(n) cout<<n.x<<" "<<n.y<<endl
intc N=505;
int h,w;
char s[N][N];
struct point {
int x,y;
int operator *(const point &p) {
return abs(p.x-x)*abs(p.y-y);
}
};
signed main() {
Cios;
cin>>h>>w;
for (int i=1;i<=h;i++) {
for (int j=1;j<=w;j++) cin>>s[i][j];
}
point p11,p12,p21,p22;
for (int i=1;i<=h;i++) {
bool bl=1;
for (int j=1;j<=w;j++) {
if (s[i][j]=='#') {
p11={i,j};
bl=0;
break;
}
}
if (!bl) break;
}
for (int i=h;i>=1;i--) {
bool bl=1;
for (int j=w;j>=1;j--) {
if (s[i][j]=='#') {
p22={i,j};
bl=0;
break;
}
}
if (!bl) break;
}
for (int i=h;i>=1;i--) {
bool bl=1;
for (int j=1;j<=w;j++) {
if (s[i][j]=='#') {
p12={i,j};
bl=0;
break;
}
}
if (!bl) break;
}
for (int i=1;i<=h;i++) {
bool bl=1;
for (int j=w;j>=1;j--) {
if (s[i][j]=='#') {
p21={i,j};
bl=0;
break;
}
}
if (!bl) break;
}
// out(p11);
// out(p22);
// out(p12);
// out(p21);
point p1,p2;
if (p11*p22>=p12*p21) {
p1=p11;
p2=p22;
}
else {
int p12x=p12.x,p12y=p12.y,p21x=p21.x,p21y=p21.y;
p1={p21x,p12y};
p2={p12x,p21y};
}
for (int i=p1.x;i<=p2.x;i++) {
for (int j=p1.y;j<=p2.y;j++) {
if (s[i][j]!='#') {
cout<<i<<" "<<j<<endl;
return 0;
}
}
}
return 0;
}C. 戴帽子
和数学沾边的就没几道好写的….
分析一下题目,可以发现,因为题目保证有解,所以整个序列肯定是由最多三个由 $0$ 开始的连续子序列组成的。所以用三个数维护当前三个序列的最大值。
答案也很好求。在每一次遍历到新数时,它能加到的序列数量就是此时的选择数。根据乘法原理,把所有的选择相乘即可。
#include<bits/stdc++.h>
using namespace std;
#define intc const int
#define int long long
#define Cios ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
intc N=1e5+10,mod=1e9+7;
int ans=1,n,a[N],t[]={0,-1,-1,-1};
signed main(){
Cios;
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=n;i++) {
int cnt=0,fj=0;
for (int j=1;j<=3;j++) {
if (t[j]+1==a[i]) {
fj=j;
cnt++;
}
}
(ans*=cnt)
if (fj>=1&&fj<=3) t[fj]++;
}
cout<<ans
return 0;
}D. 极大递增子序列
赛时是直接枚举的,但是有一点:在枚举的时候记录当前以遍历到的最小值。因为要求极长,所以往下遍历时不能出现比以前大的数,否则这个序列就不是极长的。
#include<bits/stdc++.h>
using namespace std;
#define intc const int
#define int long long
#define Cios ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
int n,cnt,a[55];
void dfs(int x) {
int min=INT_MAX;
bool fl=0;
for (int i=x+1;i<=n;i++) {
if (a[i]>a[x]&&a[i]<min) {
min=a[i];
fl=1;
dfs(i);
}
}
if (!fl) cnt++;
}
signed main(){
Cios;
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
dfs(0);
cout<<cnt;
return 0;
}事实上,这道题写到这里还没完。我们发现,dfs(i)的值一定是固定的。我们就能想到记忆化;进一步的,我们可以使用dp。只不过dp是反着操作的(欸嘿~
#include<bits/stdc++.h>
using namespace std;
#define intc const int
#define int long long
#define Cios ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
int n,a[55],dp[55];
signed main(){
Cios;
cin>>n;
dp[0]=1;
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=n;i++) {
int mx=-1;
for (int j=i-1;j>=0;j--) {
if (a[j]>=a[i]) continue;
if (a[j]>=mx) {
dp[i]+=dp[j];
mx=a[j];
}
}
}
int mx=-1,ans=0;
for (int i=n;i>=1;i--) {
if (a[i]>=mx) {
ans+=dp[i];
mx=a[i];
}
}
cout<<ans<<endl;
return 0;
}
评论(0)
暂无评论